The previous post discussed what Cosmological Red Shift is (and we defined , the red-shift parameter). The saga of cosmology begins with general speculations for thousands of years about what those points of light in the sky really were. The construction of the first telescope around 1608, followed by visual explorations (by people like Galileo) of the Moon, Venus, Jupiter, Saturn and their moons led to the increasing certainty that the heavens were made of the same materials as those found on the earth. By the way, it is indeed surprising (as you will see) that to some extent, cosmology has come full circle – it seems to appear that the heavens might be composed of different “stuff” than us on Earth.
Anyway, as I alluded to in the first post, the first mystery of modern cosmology was discovered in the light from distant galaxies. If we make the entirely reasonable assumption that those galaxies were composed of stars like our sun, the light from those stars should be similar in composition (the mix of colors etc) to the light from our sun. Of course, it was entirely reasonable to expect that some of those stars might be smaller/bigger/younger/older than our sun, so if you had a good idea of how stars produced their light, you could figure out what the light should look like. Now in the 1910’s, 1920’s, 1930s, which is the era we are talking about, people didn’t really understand nuclear fusion, so there was some speculation going on about what made the stars shine. However, one thing was clear – stars contain lots of hydrogen, so we should be able to see the colors (the wavelengths) typical of emission from hot hydrogen atoms. Vesto Slipher was the first to note that the light emitted from the hydrogen (and some other light elements) in the stars in distant galaxies appeared to be red-shifted, i.e., to be redder than expected. This was puzzling, if you expected that hydrogen and other elements had the same properties as that on the Earth. The most sensible explanation was that this was an indication the galaxies were receding away from the earth. Edwin Hubble did some more work and discovered the famous correlation, now known as Hubble’s Law – the more distant a galaxy, the faster it seemed to be receding away from us. If is the recession speed of a far-away galaxy,
is how far away it is and
is Hubble’s constant,
Hubble’s constant is currently believed to be around . A MegaParsec is a million parsecs – a parsec is a convenient distance unit in cosmology and is roughly 3.26 light years. To interpret the formula, if a galaxy were 1 MegaParsec away, it would be rushing away from us at
. In terms of miles,
is
million trillion miles.
The story of how Edwin Hubble and others discovered how away the galaxies are (the right side of this equation) is interesting in its own right and features people such as Henrietta Leavitt. This will be the subject of my next post. Probably the best discussion of this is by Isaac Asimov, in a book called “The Guide to Science – Physical Sciences”.
Getting back to our discussion, we don’t think we are somehow specially located in the Universe. This, by the way, was a philosophical principle that really traces back to the Copernican idea that the Earth wasn’t the Center of the Solar System. If we aren’t in some special place in the Universe, and if we see the galaxies receding away from us, it must be that ALL galaxies are receding from each other with a relative speed proportional to their mutual distance.
Thus was born the theory of the Expanding Universe.
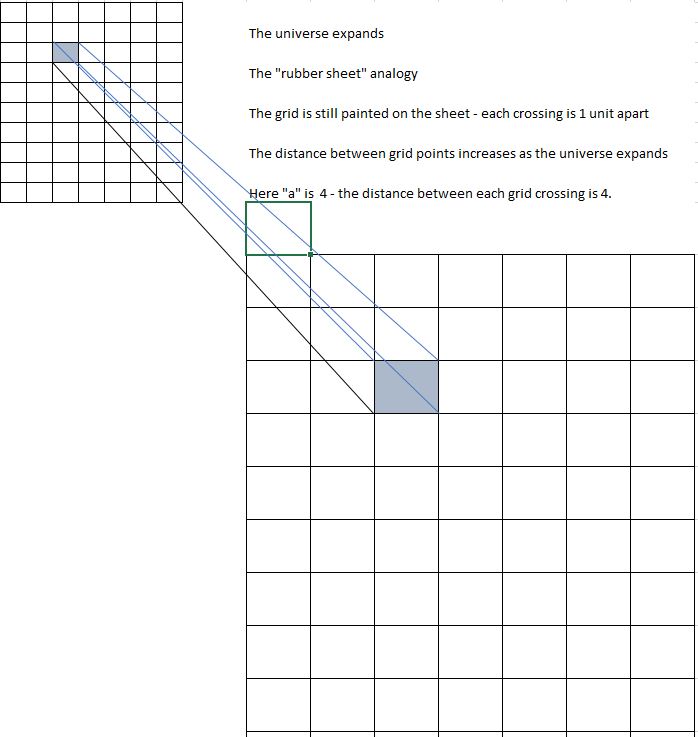
One way to think of the Expanding Universe is to think of a rubber sheet, that is being stretched from all sides. Think of a coordinate system drawn on this rubber sheet, with the coordinates actually marked . The actual distance between points on the sheet is then, not just the coordinate difference, but a “scale factor” times the coordinate difference. This “scale factor”, which is usually referred to as
in cosmological discussions, is usually assumed to be the same number for all points in space at the same point of time in the Universe’s life.

In this picture – the grid spacing is 1 as the Universe expands. However, the distance between the grid points is times the grid spacing of 1. In the picture,
is initially 1, but it increases to 4 as the expansion continues.
Next post, after I talk about distance measurements in the Universe, I’ll discuss the ideas of homogeneity and isotropy – two important concepts that we use when studying the Universe.
Leave a reply to Karthik Cancel reply